Kahoot Conceptos Básicos Unidad 3 Cultura Digital

Nuevo enlace para quienes no lo contestaron en tiempo y forma. 

Por favor antes de contestar el Kahoot, realiza lo siguiente:

1.- REPASO a tus Apuntes y al siguiente enlace 👇https://culturadigital-bachmatgdo.blogspot.com/2023/12/repaso-y-aprendo-unidad-3.html

2.-Ingresa al Kahoot "REPASO UNIDAD 3, da click a la siguiente imagen 👇 

O ingresa a  Kahoot  con el número  

03376448

¡Última oportunidad!

Plantilla para hacer Mapa Mental

Espero les sea de utilidad la siguiente plantilla, sigue los siguientes pasos:

Paso 1, dar click en el link de CANVA:

👇https://www.canva.com/design/DAF1gM6GlEI/qD_Fejqg4HLa5eMRqC7rrw/view?utm_content=DAF1gM6GlEI&utm_campaign=designshare&utm_medium=link&utm_source=publishsharelink&mode=preview

PASO 2: Dar click en Usar la plantilla para un diseño nuevo.

Paso 3: Favor de cambiar el color de fondo

Paso 4: Usar tu creatividad, no debe ser igual, agrega texto a cada ramificación  y la imagen  correspondiente.  Cambia la imagen  central.

DIAGRAMAS DE FLUJO en 2 Minutos

 

Algoritmos: Diagramas de flujo.

El análisis de un problema y la construcción de los algoritmos para solucionarlo, implican un proceso lógico que puede efectuarse de forma individual o grupal. 

Éste sólo es el primer paso de la solución, posteriormente debe revisarse para encontrar posibles errores u omisiones en la misma, pedir el punto de vista de otras personas y finalmente llevar a cabo el algoritmo. 

Cada una de estas acciones necesita, generalmente, comunicar el algoritmo a otras personas. 

En este caso, la comunicación oral del algoritmo es poco práctica porque se presentan problemas derivados de la diferencia de conceptos e incluso omisión de detalles. 

Por ello la mejor opción es utilizar herramientas que nos permiten plasmar en un lenguaje común la solución. 

Las herramientas más utilizadas para representar los algoritmos son el diagrama de flujo y el pseudocódigo.

Diagramas de flujo

Los diagramas de flujo son una herramienta para la representación gráfica de un algoritmo a través de símbolos, que corresponden a cada uno de los diferentes tipos de estructuras de control (secuencia, selección e iteración). 

Diagramas de flujo y su simbología.

Los diagramas de flujo se utilizan para describir gráficamente un algoritmo, y su simbología muestra la solución de un problema con una trayectoria de inicio a fin.

Sus características fundamentales son: 

1. El flujo de los pasos es de arriba hacia abajo y de izquierda a derecha.

• Es una secuencia de pasos:
• Inicio del proceso 
• Entrada de datos
• Proceso a realizarse
• Salida de los datos procesados y
• Fin del proceso.

2.- Existe siempre un camino que permite llegar a una solución. 

3.- Existe un único inicio del proceso. 

4.- Existe uno o más puntos de fin para el proceso de flujo. 

5.- Solamente emplea líneas de flujo horizontal y/o vertical. 

6.- Evita el cruce de líneas (usando los conectores) 

7.- Deben utilizarse los conectores sólo cuando sea necesario. 

8.- No tienen líneas de flujo sin conectar. 

9.- El lenguaje es conciso y claro.

 Estas características se representan bajo la siguiente simbología:

Las flechas son utilizadas para denotar la dirección del flujo del algoritmo flujo.

Símbolo utilizado para indicar el Inicio y el Fin del diagrama de flujo. El Inicio debe tener una línea de salida y el fin una línea de entrada (y nada más).

Símbolo utilizado para denotar la entrada salida de datos.

Símbolo usado para representar un proceso. En su interior se expresan asignaciones, operaciones aritméticas o lógicas y con datos alfanuméricos.

Cada rectángulo tiene una línea de entrada y una sola de salida sobre los puntos medios de lados distintos.

Símbolo utilizado para representar la impresión de un resultado. Expresa la escritura.

Símbolo utilizado para representar una decisión. En su interior se almacena una condición y dependiendo del resultado de la evaluación de la misma se sigue por una de las ramas o caminos alternativos.

Cada rombo debe tener una línea de entrada y dos de salida (verdadero y falso, respectivamente) sobre vértices distintos.

Dada una expresión permite escoger una opción entre muchas.

Símbolo del MIENTRAS dada una expresión al principio de la iteración, esta es evaluada. Si la condición es verdadera realizará el ciclo, si es falsa, la repetición cesará.

Símbolo DESDE/HASTA. Esta estructura de control se utiliza cuando se conoce de antemano el número de iteraciones

Símbolo REPITE HASTA. Funciona igual que la estructura MIENTRAS, con la diferencia que al menos una vez hará el grupo de instrucciones y luego evaluará una condición. Si la condición evaluada es falsa continua dentro del ciclo y si es verdadera termina la iteración.

CONECTOR dentro de página. Representa la continuidad del diagrama dentro de la misma página.

CONECTOR fuera de página. Representa la continuidad del diagrama en otra página.

Ejemplo de un diagrama de flujo

A continuación se ilustra la solución al problema que consiste en otorgar el permiso de conducir solo a personas mayores de 18 años.

18 años.

• Inicio de algoritmo
• Entrada de edad
• Decide si edad es mayor o igual a 18
• Si: Despliega “licencia otorgada”
• No: Despliega “licencia negada”
• Fin de algoritmo.

REPASO Y APRENDO UNIDAD 3.

Favor de dar click en los siguientes métodos:

• Aprende divide y vencerás
• Diagramas de flujo.
• Método Divide y Vencerás
• Método Científico.
• Método de Casos
• Método del árbol de causa
• Método del árbol de causas: recolección de la info...
• Método de Árbol de causas.
• Modelo de procesamiento de información que consta ...
• Solución creativa de problemas (SCP)

• Fases del Método de "El caso" .
• Divide y Vencerás
• Modelo de las 5 "E"
• Método de resolución de problemas es el de Bransfo...
• Método IDEAL
• 4 pasos de Polya.

• Problemas más comunes en el uso de la web
• EL SURGIMIENTO DEL DÍA DEL INTERNAUTA
• LA PRIMERA PÁGINA WEB DE LA HISTORIA QUE PUDO VISI...
• Internauta
• Historia del internet
• En el caso de Internet, destacamos los siguientes ...

Recursividad - Recursión

 

Aprende divide y vencerás

 

Pseint online en android

 

Diagramas de flujo.

Los diagramas son elementos de gran importancia en la descripción de procesos. En las lecturas anteriores pudiste comprender que los diagramas son representaciones de acciones, pasos o tareas que tienen una relación de orden. 

Por ejemplo, el proceso de alimentarnos requiere una serie de actividades como hacer la comida, servirla, comer, levantar los utensilios y lavarlos. Sería complicado variar el orden de estas actividades porque el proceso puede fallar y correr el riesgo de no cumplir con el objetivo. 

El siguiente esquema muestra el proceso que acabamos de mencionar; intenta cambiar la posición de una actividad y mira como el diagrama te apoya con las posibilidades.

Flujo de proceso: 

Imagina que las carreteras no tengan definido cómo deben ocuparse los carriles. 

Por regla, en nuestro país los conductores deben tomar el carril de la derecha, por lo tanto, al encontrarse de frente con otro vehículo cada quién se encuentra en su lugar y podemos transitar sin ningún problema. 

El flujo es la dirección o el orden que deben seguir las actividades de cierto proceso para que se pueda lograr el objetivo. Define las relaciones entre las tareas, es decir, cuál debe ejecutarse antes y cuál después.

Diagramas de Flujo

 Los diagramas de flujo, también llamados diagramas de actividades permiten diagramar procesos, representando los flujos (orden) en que deben ejecutarse las tareas. 

Estos diagramas pueden ser utilizados en cualquier ámbito, tal como lo define Manene (2011) “un diagrama de flujo es una representación gráfica que desglosa un proceso en cualquier tipo de actividad a desarrollarse tanto en empresas industriales o de servicios y en sus departamentos, secciones u áreas de su estructura organizativa”. 

Desde luego, para que los procesos puedan ser comprendidos de forma universal, los diagramas usan símbolos estandarizados que representan una acción y al visualizar el diagrama, podemos leer el proceso con una sola interpretación. 

Los símbolos utilizados en los diagramas de flujo son los siguientes:

Aunque existen más símbolos, los más usados para iniciar en el diagramado de procesos son los que se describen a continuación.

Reglas de uso: 

1. Debe tener un solo inicio y un fin. 

2. Debe construirse de arriba hacia abajo o de izquierda a derecha. 

3. Las líneas de flujo debe ser rectas, ya sea verticales u horizontales. 4. Redactar bien los enunciados para evitar confusiones. 

5. Si el diagrama es extenso, se utilizan conectores para indicar la continuidad del desarrollo del proceso. 

6. No se puede obtener de un mismo proceso dos resultados diferentes. 

Ejemplo 1. Enviar un mensaje por WhatsApp

1. Abrir APP. → Inicio 

2. Seleccionar contacto. → Proceso 

3. Escribir mensaje. → Proceso 

4. Enviar mensaje. → Proceso 

5. Fin. → Fin

Ejemplo 2. Números positivos o negativos. 

En algunas aplicaciones matemáticas es importante saber si un número es positivo o si es negativo. 

 Por ejemplo, consideremos la temperatura del agua y la unidad de medida en grados Celsius (°C); cuando el ambiente está a 0° C o menos, el agua se congela (hielo); si la temperatura es mayor a 0° C el agua no se congela. 

En otras palabras, si el valor de la temperatura es negativo el agua se congela, pero si el valor es positivo no llega al punto de congelación y se queda líquida. 

Si tomamos en cuenta estos datos en la recta numérica, notamos cómo los números negativos están a la izquierda del 0 y los positivos están a la derecha.

NOTA. Hacemos la aclaración que por definición el agua se congela a 0° C, sin embargo, el cero no es ni negativo ni positivo, es un número neutro, por lo que no lo consideraremos en este ejemplo. 

Con el sentido de las flechas, podemos recordar fácilmente la simbología de los positivos y los negativos. 

Como se muestra en la figura los positivos se representan con la flecha que apunta hacia la derecha y los negativos con la flecha en sentido hacia la izquierda. 

Si solo dejamos las puntas de las flechas, obtenemos las figuras del inciso b); acomodando las X con respecto al cero, obtenemos la representación matemática de los números negativos ( x < 0 ) y los positivos ( x > 0 ), donde el símbolo “<” significa “menor que” y se lee como “x es menor que 0” y el símbolo “>” significa “mayor que”, se lee como “x es mayor que cero”.

Existen varias formas de expresar a los números positivos y los negativos con el ejemplo de la temperatura del agua. 

Lenguaje natural 

• Cuando el agua está a una temperatura menor a 0° C se congela. 

• Si la temperatura es mayor a 0° C el agua no se congela. 

Lenguaje matemático 

Sea x el valor de una temperatura en grados Celsius 

• El agua se congela si: { x : x < 0 } 

• El agua no se congela si: { x : x > 0 } 

Lenguaje algorítmico 

Si x < 0 entonces El agua se congela Sino El agua no se congela 

El lenguaje algorítmico pareciera que toma en cuenta una sola opción ( x < 0 ) y no se considera cuando x > 0, sin embargo está incluida en el SINO, la cual indica que si la temperatura NO es menor que cero, entonces es mayor que cero. 

El siguiente esquema muestra los posibles estados del agua cuando se encuentra a cierta temperatura. 

Al asignar un valor a la temperatura (representado por la letra C) podemos compararlo con el cero; si C es menor que cero, es decir es negativo, el agua se congela; si C no es menor que cero (positivos), entonces el agua no se congela.

Supongamos que C toma el valor positivo 15, es decir C = 15, de acuerdo con nuestro proceso evaluamos ¿15 es menor que cero? 

La respuesta es NO, por lo tanto, obtendríamos el resultado “No se congela”. 

Veamos el caso con un número negativo. 

C = -2, evaluamos ¿ -2 es menor que 0? 

La respuesta es SI, entonces el resultado del proceso es “Se congela”. 

Con este análisis, el diagrama de flujo del proceso que determina si el agua se congela o no con determinada temperatura es el siguiente: 

Método Divide y Vencerás

 

Este proceso se puede repetir en cada subproblema que surja, dividiéndolo aún más en subproblemas más pequeños hasta que se puedan resolver fácilmente. 

La ventaja del método "Divide y Vencerás" es que puede reducir significativamente el tiempo y la complejidad de la resolución de problemas. 

Problema: Una empresa de transporte necesita optimizar su ruta de entrega para minimizar el tiempo de entrega y los costos asociados. 

Solución con el método "Divide y Vencerás": 

En este caso, el método "Divide y Vencerás" ha permitido a la empresa de transporte resolver un problema complejo y reducir su tiempo y costos de entrega mediante la división del área de entrega en zonas manejables y la optimización de las rutas de entrega en cada zona de forma independiente. 

Método Científico.

El método científico es un modelo para la resolución de problemas en la investigación científica. Este método se utiliza para diseñar y llevar a cabo experimentos y observaciones para probar hipótesis y teorías científicas generalmente implica los siguientes pasos:

1. OBSERVACIÓN. Observar un fenómeno o problema que requiere explicación

2. HIPÓTESIS. Propone una hipótesis para explicar el fenómeno o problema observado.

3. EXPERIMENTO. Diseñar un experimento o serie de observaciones para probar la hipótesis.

4. RECOPILACIÓN DE DATOS. Colecciona datos a partir de los experimentos u observaciones.

5. ANÁLISIS DE DATOS. Analiza los datos para determinar si la hipótesis es compatible con los resultados experimentales u observacionales.

6. CONCLUSIONES. Concluye si la hipótesis es válida o no en función de los resultados experimentales u observacionales.

7. COMUNICACIÓN DE RESULTADOS. El científico comunica los resultados del experimento u observación a otros científicos mediante publicaciones científicas o presentaciones en conferencias

Este proceso puede repetirse varias veces, clarificando la hipótesis y el diseño del experimento hasta que se logren conclusiones sólidas y validadas.

Un ejemplo clásico de aplicación del método científico Es el experimento de Louis Pasteur que demostró la falsedad de la teoría de la generación espontánea y estableció la teoría de la biogénesis. La teoría de la generación espontánea sostenía que ciertos seres vivos, como los gusanos, las moscas o las bacterias, surgían de manera espontánea a partir de materia orgánica en descomposición. Pasteur no creía en esta teoría y decidió diseñar un experimento para probar su hipótesis de que la vida solo puede provenir de la vida preexistente.

1.       OBSERVACIÓN.

Observar la materia orgánica en descomposición.

Aparición de microorganismos en el caldo.

2.       HIPÓTESIS.

La vida solo puede provenir de la vida preexistente.

3.       EXPERIMENTACION.

Pasteur preparó dos frascos de cuello largo y estrecho, los cuales llenó con un caldo nutritivo.

El primer frasco lo dejó abierto, permitiendo que el aire contaminado con microorganismos pudiera entrar en contacto con el caldo, mientras que el segundo frasco lo selló herméticamente, impidiendo el contacto del aire con el caldo.

4.       RECOPILACIÓN DE DATOS.

Pasaron varios días y el caldo del primer frasco se llenó de microorganismos, mientras que el segundo frasco permaneció estéril.

5.       ANÁLISIS DE DATOS.

Aparición de microorganismos en el caldo del frasco tapado y el abierto.

6.       CONCLUSIONES.

La teoría de la generación espontánea era falsa. COMUNICACION DE RESULTADOS. Pasteur demostró que la vida solo puede provenir de la vida preexistente.

Método de Casos

 

A través de la discusión de casos, los estudiantes pueden: 

 1. Adquirir conocimientos. 

Conceptos, Teorías y Técnicas 

2. Desarrollar habilidades. 

Al discutir situaciones de la vida real, los participantes ejercitan ciertas habilidades que le resultarán indispensables para el desempeño profesional. 

• Pensamiento crítico 

• Capacidad de análisis, síntesis, evaluación 

• Argumentación 

• Toma de decisiones 

• Interactuar con otras personas 

• Comunicación verbal 

3. Formar actitudes. 

La exposición a diferentes modos de ver una misma situación motiva al participante a reexaminar sus propias actitudes y valores. 

• Flexibilidad ante las diferencias personales 

• Seguridad • Sensibilización a necesidades del entorno 

• La comprensión de fenómenos y hechos sociales mediante el acercamiento con la realidad

Ejemplo:

Método del árbol de causa

 

Método del árbol de causas: recolección de la información y forma que tomará el árbol

 

Método de Árbol de causas.

 El método árbol de causas persigue evidenciar las relaciones entre los hechos que han contribuido en la producción del accidente. 

La pregunta clave es "¿Qué tuvo que ocurrir para que este hecho se produjera?". 

Se persigue reconstruir las circunstancias que había en el momento inmediatamente anterior al accidente y que permitieron o posibilitaron la materialización de este. 

ETAPAS DE LA APLICACIÓN DEL MÉTODO DEL ÁRBOL DE CAUSAS 

PRIMERA ETAPA: Recolección de la información. 

SEGUNDA ETAPA 

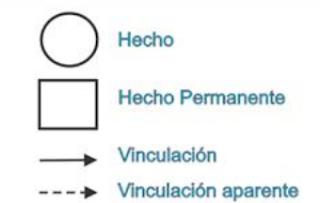
Construcción del Árbol Entonces utilizaremos los siguientes elementos para construir el Árbol: 

Ahora comenzaremos a vincular los hechos de derecha a izquierda partiendo del último hecho y ante poniendo el hecho que tuvo que ocurrir para que suceda el anterior, para ello nos deberemos de hacer 3 preguntas: 

1. ¿Cuál fue el último Hecho? 
2. ¿Que fue necesario para que se produzca este último hecho? 
3. ¿Fue necesario algún otro hecho más? 

La vinculación podrá representarse de las siguientes formas:

Vinculación: Para que ocurra el hecho «B» fue necesario que ocurriera el hecho «A». }

Ejemplo: Para que el piso se encuentre mojado (B) fue necesario que lloviera(A). 

Conjución: Para que ocurra el hecho «C» fue necesario que ocurrieran los hechos «A» y «B». 

Ejemplo: 

Para que leas este articulo (C) fue necesario que lo Nosotros lo Publicáramos (A) y que tú lo hayas encontrado (B). 

Disyunción: Para que ocurran los hechos «C» y «B» fue necesario que ocurra el hecho «A», en este caso dos hechos ocurren por una sola causa. 

Ejemplo: Para que tu automóvil se dañe (C) y tú te lastimes (B), fue necesario que chocaras (A). 

TERCER ETAPA

Gestión de la Información Descripción del accidente

En una empresa dedicada a la fabricación de pan y situada en las afueras de una población, se efectúa diariamente el reparto de los productos fabricados en jornada de noche, para lo cual, el conductor-repartidor utiliza el camión de reparto de la empresa. 

 El día del accidente, dicho conductor, al ir a poner en marcha el camión, se encuentra con que no arranca, razón por la cual decide utilizar una furgoneta antigua, también de la empresa, y que se utiliza excepcionalmente como auxiliar. Ordena que carguen la furgoneta, y aunque se da cuenta que el pedido del día es mayor del habitual, decide sobrecargarla para no tener que efectuar dos viajes. 

Al salir de la fábrica, se encuentra con que la vía que conduce a la ciudad está colapsada debido a la lluvia, razón por la cual decide tomar una carretera secundaria en la que existen pendientes pronunciadas. 

Al descender por una de dichas pendientes, no le responden adecuadamente los frenos y choca con un árbol, resultando gravemente herido. La mencionada furgoneta no se somete al mantenimiento que se efectúa en el camión de reparto, y una posterior revisión, demostró que los frenos estaban en mal estado.

Relación de hechos La relación de hechos que se deducen de la anterior descripción se proporciona en la tabla siguientes.

Confección del árbol de causas Partiendo de la lesión grave del conductor tendremos: 

P: ¿Qué fue necesario para que se produjese la lesión grave? 

R: Chocar la furgoneta contra un árbol

P: ¿Ha sido necesario otro hecho? R No. Luego entre ambos hechos, lesión y choque forman una relación de cadena: P: ¿Qué fue necesario para chocar contra el árbol? R: Que no respondieran adecuadamente los frenos. P: ¿Fue necesario algo más? R: No

Entre ambos hay una relación de cadena: 

P: ¿Qué fue necesario para que no respondan bien los frenos? 

 R: Frenos en mal estado. 

 P: ¿Fue necesario algo más? 

R: Si, Fuerte pendiente. 

 P: ¿Fue necesario algo más? 

R: Si, Sobrecarga de la furgoneta. 

 P: ¿Fue necesario algo más? 

R: No. 

Entre ellos hay una conjunción.

Ahora se analizan cada una de las ramas anteriores. 

P: ¿Que ha sido necesario para utilizar una fuerte pendiente? 

R: Toma de vía alternativa. 

 P: ¿Ha sido necesario otro hecho? 

R: no. Existe una relación de cadena 

P: ¿Qué tuvo de pasar para que tomase la vía alternativa? 

R: Que la vía usual estuviera colapsada 

 P: ¿Ha sido necesario otro hecho? 

R: No 

Hay una relación de cadena entre hechos 

P: ¿Qué fue necesario para que la vía usual estuviera colapsada? 

R: Que llueva El siguiente hecho a analizar sería la lluvia y nos preguntaríamos, ¿Qué tiene que suceder para que llueva? 

Luego se pondría un interrogante, ¿ya que, aunque tenga causas básicas no profundizamos.

El siguiente hecho a analizar seria, frenos en mal estado: 

P: ¿Qué tuvo que ocurrir para que los frenos estuvieran en mal estado? 

R: Que usase la furgoneta auxiliar. 

P: ¿Ha sido necesario otro hecho? 

R: La falta de revisión de la furgoneta. 

P: ¿Ha sido necesario otro hecho? 

R: No. Existe una conjunción entre los hechos

Frenos en mal estado 

Falta de revisión. 

Furgoneta auxiliar. 

 Analizaremos ahora la falta de revisión de la furgoneta: 

 P: ¿Qué ha sido necesario para que no se revise la furgoneta? 

R: No se tiene respuesta. Luego se pondría un interrogante 

P: ¿Qué ocurrió para usar la furgoneta auxiliar? 

R: Que no arrancase el camión. Hay una relación de cadena entre los hechos. Analicemos camión no arranca. 

P: ¿Qué ocurrió para que el camión no arrancase? 

R: No se tiene información. Se pondría una interrogación, El último hecho a analizar seria la sobrecarga. 

P: ¿Qué ocurrió para que se sobrecargase la furgoneta? 

R: Evitar un segundo viaje. 

P: ¿ha sido necesario otro hecho? 

R: No. 

Luego hay una relación de cadena: 

Del hecho evitar un segundo viaje no se tiene más información, luego acabaría en interrogante. Se termina así de finalizar el árbol, al identificar las causas primarias o causas que propiciaron las causas del accidente, no precisan de una situación anterior para ser explicadas, o bien debido a una toma de datos incompleta o incorrecta, se desconocen los antecedentes que proporcionaron una determinada situación del hecho. La representación total del árbol de causas de nuestro ejemplo queda recogida en la siguiente figura:

Se ha llegado así a establecer unas causas que determinan el que se produzca el accidente, por lo tanto, para evitar éste o un accidente similar en el futuro, bastará con eliminar alguna, y con ello, se rompe la cadena causal. 

Entre las causas que determinan la aparición del accidente, hay que distinguir entre causas primarias y causas secundarias, siendo estas últimas aquellas sobre las que no se podría actuar, como es el tema de la lluvia en el accidente considerado. 

En el caso, al considerar las causas principales, si por ejemplo se establecen revisiones periódicas para la furgoneta auxiliar, evitaremos que se vuelva a producir el accidente descrito, ahora bien, desde el punto de vista prevencionista, el estudio de los hechos que han dado Iugar a Ia aparición de un accidente, nos sirve para ponernos en guardia y ampliar nuestro punto de vista preventivo; de esta manera, volviendo al caso estudiado, el no efectuar revisiones periódicas a la furgoneta puede ponernos sobre aviso de si las mismas circunstancias se dan con otros equipos, maquinaria, etc., 

Lo que a su vez podría ser la causa de otros tipos de accidentes. 

Aplicación de medidas correctoras

Una vez determinadas las causas del accidente, es necesario el proponer unas medidas correctoras, las cuales deben tener unas características tales como: 

• No perder su efectividad al poco tiempo.
• No introducir operaciones suplementarias para el operario.
• No generar nuevos peligros.
• Que alcance al mayor número de problemas presentes.
• Que sea factible de establecer.

Métodos para la resolución de problemas computacionales

 Autor :Thompson (1996)

Fases

 • Entender el problema. 

• Diseñar el problema. 

• Escribir el programa.

 • Evaluar la solución.

 Autor :Mac Gaul de Jorge et al. (2008)

Fases

 Comprender el problema implica: 

• Reconocer términos. 

• Identificar entradas, salidas, condiciones. 

• Diseñar casos prueba. 

• Seleccionar componentes (concebir un plan conectando con los conocimientos previos adquiridos, identificando los conceptos necesarios para resolver el problema).

• Diseñar el algoritmo. 

• Prueba de escritorio.

Modelo de procesamiento de información que consta de un espacio de problema

 Autor:Newell y Simon (1972) 

Modelo heurístico:Modelo de procesamiento de información que consta de un espacio de problema 

• Estado inicial 

• Estado final 

• Vías de solución posibles 

¿Cómo funciona?

Quien resuelve el problema se forma una representación de este y realiza operaciones para reducir la discrepancia entre el estado inicial y el final.

Solución creativa de problemas (SCP)

 Autor:Treffinger (1985) y Treffinger e Isaksen (2005)

 Modelo heurístico:  Solución creativa de problemas (SCP) 

1. Entender el problema. 
2. Generar ideas. 
3. Prepararse para la acción. 

¿Cómo funciona?

1. La comprensión del problema inicia con una meta general para la solución de problemas. Se deben obtener datos importantes como: hechos, opiniones y preocupaciones para formular una pregunta específica. 
2. La clave para generar ideas es el pensamiento divergente, el cual es capaz de producir diversas opciones que conduzcan a lograr la meta planteada. 
3. Prepararse para la acción incluye examinar las opciones más promisorias y buscar fuentes de ayuda o maneras para superar la resistencia.

Asignar y editar título de una presentación Genially.

 Favor de dar click en la siguiente imagen 

                               👇 

Cómo añadir o cambiar tu foto o vídeo de perfil:

 

1. Pulsa en Perfil en la esquina inferior derecha.

2. Pulsa Editar perfil.

3. Pulsa Cambiar foto o Cambiar video.

4. Opción «Cambiar foto»: selecciona Hacer una foto o Cargar foto. Opción «Cambiar video»: selecciona un video de la galería.